머신러닝 시스템을 분류하는 또다른 방법은 입력 데이터의 stream으로부터 점진적으로 학습할 수 있는지의 여부에 따라 batch learning와 online learning으로 구분하는 것이다.
Batch Learning
batch learning에서는 시스템이 점진적으로 학습할 수 없다. 가용한 데이터를 모두 사용해서 훈련해야 하며 일반적으로 많은 시간과 자원을 소모하므로 보통 오프라인 환경에서 수행된다. batch learning에서 새로운 데이터가 들어왔을 때 새로운 데이터뿐만 아니라 이전 데이터도 포함한 전체 데이터에 대해 학습시켜야 한다. 그런 다음 이전 시스템을 중지시키고 새 시스템으로 교체한다.
Oneline Learning
oneline learning에서는 데이터를 순차적으로 한개씩 또는 mini-batch 단위로 주입하여 시스템을 학습시킨다. 매 학습 단계가 빠르고 비용이 적게 들어 시스템은 데이터가 도착하는 대로 즉시 학습할 수 있다. 새로운 데이터가 들어왔을 때 처음부터 전부 학습시키는 것이 아닌 그 부분만을 학습시킬 수 있어서 유용하다. oneline learning은 연속적인 데이터를 받고 빠른 변화에 스스로 적응해야 하는 시스템에 적합하다.
Regularization
regularization(정규화)는 overfitting을 막기 위함이다. 그전에 underfitting과 overfitting에 대해 다시 한번 알아보자. [Supervised Learning] Regression① 에서 짧게 언급했듯이, underfitting은 hypothesis가 data를 잘 설명하지 못하는 것이다. 이는 주로 복잡한 non-linear data를 linear model로 fitting할 때 나타나며, 예측 성능이 낮게 나오는 경향이 있다. 반면, overfitting은 hypothesis가 data를 완전히 외워버린 것이다. 주어진 데이터에 대해서는 아주 정확하게 예측하지만 처음 보는 데이터(unseen data)에 대해서는 제대로 예측하지 못하여 성능이 낮다. 이는 generalization(일반화)의 관점에서 좋지 않다. 여기서 generalization은 test data에 대해 높은 성능을 갖는 것이다.

error를 판단할 때 고려하는 요소들 중 bias와 variance가 있다.
- bias : 데이터 내에 모든 정보를 고려하지 않고 지속적으로 잘못된 것을 학습하는 경향으로, train data를 바꿈에 따라 알고리즘의 정확도가 얼마나 많이 변화하는지를 나타낸다. 보통 underfitting에서 데이터 내의 모든 정보를 고려하지 못하므로, 높은 bias가 나타난다. 반면, overfitting에서는 낮은 bias가 나타난다.
- variance : 학습 데이터에 highly flexible하게 fitting된 모델을 구성하여 random한 것까지 학습하는 경향으로, 특정 input data에 알고리즘이 얼마나 민감한지를 나타낸다. 이는 unseen data에 대해 모델이 얼마나 많이 변하는지로도 나타낼 수 있다. 보통 overfitting에서 높은 variance가 나타나 generality가 부족하다고도 하며, underfitting에서는 낮은 variance가 나타난다.
이러한 요소들을 활용하여 Error(X) = noise(X) + bias(X) + variance(X) 로 나타낸다.
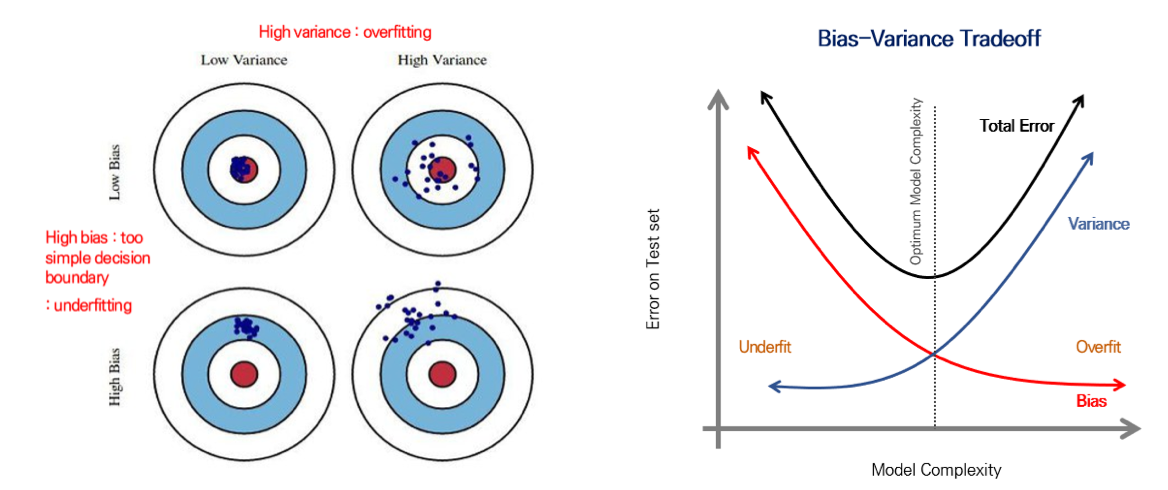
bias와 variance는 서로 trade off 관계를 갖고 있어, 적당한 bias와 적당한 variance를 가지는 경계에서 total error가 최소인 지점이 발생하며 이 지점이 최적이다. [Supervised Learning] Regression① 의 cross validation 부분에서 다뤘던 그래프처럼 모델의 복잡도가 증가하면서 test data에 대한 error가 감소하다가 어느 순간부터 generality를 잃어버리면서 error가 증가하게 되는 반면, train data에 대한 error는 계속해서 학습하면서 해당 데이터를 외워버리기 때문에 점점더 error가 감소한다. 따라서 이 두가지를 모두 고려해야 하는데, test error(out-of-sample error)와 train error(in-sample error)의 차이가 클 수록 generalization performance가 안좋으며, test error가 다시 증가하는 부분부터는 해당 차이를 overfitting된 정도로 볼 수있다.
Overfitting Solution
1. More train data: generality를 높이는 가장 좋은 방법은 더 많은 train data를 모으는 것이다. 직접 수집할 수도 있지만 비현실적이고 데이터의 양은 제한되어 있다. 그래서 fake data를 만들어 train dataset에 추가하는 방법이 제안되었다. data augmentation는 input에 noise를 주입하는 방법이다. 이는 generalization error를 극적으로 줄일 수 있다.
2. Regulation: 모델이 주어진 데이터에 대해 과도한 학습을 하지 못하도록 직접 규제한다.
- architecture 측면에서는 hidden layers and units per layer 수를 줄이는 방법이 있다.
- Early Stopping: batch를 minibatch 단위로 끊어서 학습하면서 validation set error를 확인하여 overfitting하기 전에 학습을 멈추는 방법이다.
- Weight-decay: L1 penalty(절댓값) 혹은 L2 penalty(제곱)으로 큰 weight에 penalty를 주는 방식이다. 특정이 모델을 외워 bending이 나타나면 overfitting이므로, spread model에는 weight에 작은 값을 주고 bend model에는 weight에 큰 값을 주고 cost function에서 이를 조정하는 것이다. $$L=\frac{1}{N}\sum_i D(S(WX_i+b),L_i)+\lambda \sum W^2$$ 이와 같이 $\lambda \sum W^2$이라는 regularization term을 주면서 weight가 커지면 cost가 커지고 학습은 cost를 감소시키는 방향으로 진행되므로 penalty 역할을 하게 되는 것이다. 이때, $\lambda$는 regularization의 강도를 의미하며 0이면 regularization을 사용하지 않고 1이면 아주 중요하게 사용하는 것이다. 만약 $\lambda$가 너무 커지게 되면 underfitting이 발생하게 되므로 적절한 $\lambda$를 설정하는 것이 중요하다. 모든 parameter에 대해 적용하지 않고 일부 parameter에 대해서만 regularization을 적용할 수도 있다.
- L2 parameter regularization: $\tilde{J}(w;X,y)=\frac{\alpha}{2}w^Tw+J(w;X,y)$
- L1 parameter regularization: $\tilde{J}(w;X,y)=\alpha ||w||_1+J(w;X,y)$
- Drop Out: 모델 복잡도(hidden layer의 개수, hidden layer 각각의 node의 개수)가 정해진 상황에서 parameter 수가 고정되어 있는데, parameter 수가 많으면 overfitting이 발생하므로 이를 해결하기 위해서 학습 중간중간에 parameters를 끊어주는 것이다. 즉, 학습하는 과정에서 특정 node를 deactivate하는 것이다.
- Drop-connect: neurons(nodes)를 끄는 drop out과 달리, neurons(nodes) 사이의 연결을 끊어버리는 것이다.
- Batch Normalization: 각 activation 별로 train할 때에는 mini-batch의 평균과 분산으로, test할 때에는 계산해둔 이동 평균으로 normalize하고 이후 scale factor와 shift factor를 이용해서 새로운 값을 만들어 내놓으면 이들을 다른 backpropagation에서 학습하는 방식이다. 이 방식의 장점은 학습속도가 빠르고 dropout이나 L2 weight decay를 할 필요없다는 것이다. 하지만 너무 비슷한 분포로 나타나 representation capacity가 떨어진다는 단점이 있다. (batch축 $\rightarrow$ $\frac{\sum}{batch수}$)
- Layer Normalization: Batch Normalization과 유사하나, 특정 batch 내의 layer안에서 혹은 channel 안에서 normalize하는 방식이다. (layer축 $\rightarrow$ $\frac{\sum nodes}{layer 속 node 수}$)

3. Reduce # of feature: 불필요한 input variables(features)를 줄이는 것도 regularization에 도움이 될 수 있다.
4. Ensemble: 다른 모델들의 평균을 내는 것이다.
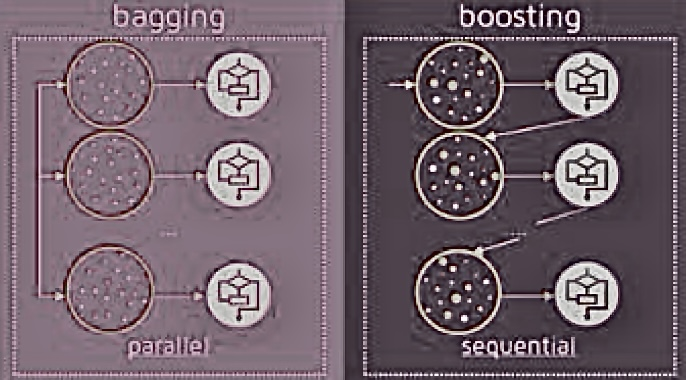
- Bagging: n개의 datasets으로 나눠서 n개의 모델을 학습시킨 후 simple average를 구하는 것이다.
- Boosting: 모델들 사이의 순서를 정해서 다음 모델은 앞 모델이 학습한 결과의 error에 집중하여 학습하도록 한 후 weighted average를 구하는 것이다.
[출처] 한양대학교 장준혁 교수님 인공지능개론 수업
'인공지능' 카테고리의 다른 글
| [인공지능개론] CNN② (0) | 2024.05.08 |
|---|---|
| [인공지능개론] CNN① (0) | 2024.05.08 |
| [인공지능개론] Neural Networks② (0) | 2024.05.08 |
| [인공지능개론] Neural Networks① (0) | 2024.05.07 |
| [인공지능개론] Regression④ (0) | 2024.05.07 |




댓글